Ang mga natural na phenomena at proseso sa paligid natin ay medyo kumplikado. Para sa kanilang eksaktong pisikal na paglalarawan, ang isang masalimuot na kasangkapang pangmatematika ay dapat gamitin at isang malaking bilang ng mga makabuluhang salik ang dapat isaalang-alang. Upang maiwasan ang problemang ito, ang ilang mga pinasimple na modelo ay ginagamit sa pisika, na lubos na nagpapadali sa pagsusuri sa matematika ng proseso, ngunit halos hindi nakakaapekto sa katumpakan ng paglalarawan nito. Ang isa sa kanila ay ang perpektong modelo ng gas. Isaalang-alang natin ito nang mas detalyado sa artikulo.
Ang konsepto ng ideal na gas
Ang ideal na gas ay isang estado ng pagsasama-sama ng isang substance, na binubuo ng mga materyal na punto na hindi nakikipag-ugnayan sa isa't isa. Ipaliwanag natin ang kahulugang ito nang mas detalyado.
Una, pinag-uusapan natin ang mga materyal na punto bilang mga bagay na bumubuo ng perpektong gas. Nangangahulugan ito na ang mga molekula at atomo nito ay walang sukat, ngunit may tiyak na masa. Ito ay matapangmaaaring gumawa ng pagtatantya na isinasaalang-alang ang katotohanan na sa lahat ng tunay na gas sa mababang presyon at mataas na temperatura, ang distansya sa pagitan ng mga molekula ay mas malaki kaysa sa kanilang mga linear na dimensyon.
Pangalawa, ang mga molecule sa isang ideal na gas ay hindi dapat makipag-ugnayan sa isa't isa. Sa katotohanan, palaging umiiral ang gayong mga pakikipag-ugnayan. Kaya, kahit na ang mga atomo ng noble gas ay nakakaranas ng dipole-dipole attraction. Sa madaling salita, naroroon ang mga pakikipag-ugnayan ng van der Waals. Gayunpaman, kumpara sa kinetic energy ng pag-ikot at pagsasalin ng paggalaw ng mga molekula, ang mga pakikipag-ugnayan na ito ay napakaliit na hindi ito nakakaapekto sa mga katangian ng mga gas. Samakatuwid, hindi sila maaaring isaalang-alang kapag nilulutas ang mga praktikal na problema.
Mahalagang tandaan na hindi lahat ng gas kung saan mababa ang density at mataas ang temperatura ay maituturing na perpekto. Bilang karagdagan sa mga interaksyon ng van der Waals, may iba pang mas malakas na uri ng mga bono, halimbawa, mga hydrogen bond sa pagitan ng mga molekula ng H2O, na humahantong sa isang matinding paglabag sa mga kondisyon ng ideality ng gas. Para sa kadahilanang ito, ang singaw ng tubig ay hindi isang perpektong gas, ngunit ang hangin ay.
Pisikal na modelo ng perpektong gas
Maaaring katawanin ang modelong ito bilang mga sumusunod: ipagpalagay na ang sistema ng gas ay naglalaman ng N particle. Ang mga ito ay maaaring mga atomo at molekula ng iba't ibang kemikal at elemento. Ang bilang ng mga N particle ay malaki, kaya ang yunit na "mole" ay karaniwang ginagamit upang ilarawan ito (1 mole ay tumutugma sa numero ni Avogadro). Lahat sila ay gumagalaw sa ilang volume na V. Mga paggalaw ng butilay magulo at malaya sa isa't isa. Bawat isa sa kanila ay may tiyak na bilis v at gumagalaw sa tuwid na daan.
Sa teorya, ang posibilidad ng banggaan sa pagitan ng mga particle ay halos zero, dahil maliit ang laki ng mga ito kumpara sa mga interparticle na distansya. Gayunpaman, kung nangyari ang naturang banggaan, kung gayon ito ay ganap na nababanat. Sa huling kaso, ang kabuuang momentum ng mga particle at ang kanilang kinetic energy ay natipid.
Ang itinuturing na modelo ng mga ideal na gas ay isang klasikal na sistema na may malaking bilang ng mga elemento. Samakatuwid, ang bilis at enerhiya ng mga particle sa loob nito ay sumusunod sa istatistikal na pamamahagi ng Maxwell-Boltzmann. Ang ilang mga particle ay may mababang bilis, habang ang iba ay may mataas na bilis. Sa kasong ito, mayroong isang tiyak na makitid na limitasyon ng bilis, kung saan ang pinaka-malamang na mga halaga ng dami na ito ay namamalagi. Ang velocity distribution ng nitrogen molecules ay ipinapakita sa schematically sa ibaba.
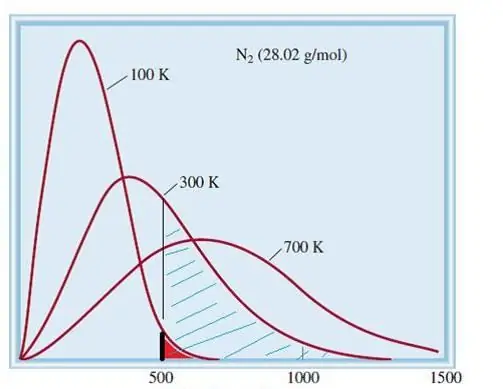
Kinetic theory of gases
Ang modelo ng mga ideal na gas na inilarawan sa itaas ay natatanging tinutukoy ang mga katangian ng mga gas. Ang modelong ito ay unang iminungkahi ni Daniel Bernoulli noong 1738.

Kasunod nito, binuo ito hanggang sa kasalukuyang estado ni August Kroenig, Rudolf Clausius, Mikhail Lomonosov, James Maxwell, Ludwig Boltzmann, Marian Smoluchowski at iba pang mga siyentipiko.
Ang kinetic theory ng mga fluid substance, na batayan kung saan binuo ang perpektong modelo ng gas, ay nagpapaliwanag ng dalawang mahalagang macroscopic na katangian ng system batay sa microscopic na pag-uugali nito:
- Ang presyon sa mga gas ay resulta ng pagbangga ng mga particle sa mga dingding ng sisidlan.
- Ang temperatura sa system ay resulta ng pagpapakita ng patuloy na paggalaw ng mga molekula at atomo.
Palawakin natin ang parehong konklusyon ng kinetic theory.
Gas pressure
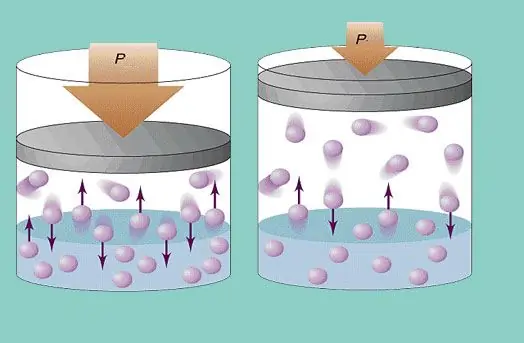
Ang perpektong modelo ng gas ay ipinapalagay ang isang patuloy na magulong paggalaw ng mga particle sa system at ang kanilang patuloy na pagbangga sa mga dingding ng sisidlan. Ang bawat naturang banggaan ay itinuturing na ganap na nababanat. Maliit ang particle mass (≈10-27-10-25 kg). Samakatuwid, hindi ito maaaring lumikha ng maraming presyon sa isang banggaan. Gayunpaman, ang bilang ng mga particle, at samakatuwid ang bilang ng mga banggaan, ay napakalaki (≈1023). Bilang karagdagan, ang root mean square velocity ng mga elemento ay ilang daang metro bawat segundo sa temperatura ng silid. Ang lahat ng ito ay humahantong sa paglikha ng kapansin-pansing presyon sa mga dingding ng sisidlan. Maaari itong kalkulahin gamit ang sumusunod na formula:
P=Nmvcp2 / (3V), kung saan ang vcp ay root mean square velocity, m ay particle mass.
Ganap na temperatura
Ayon sa ideal na modelo ng gas, ang temperatura ay natatanging tinutukoy ng average na kinetic energy ng isang molekula o atom sa system na pinag-aaralan. Maaari mong isulat ang sumusunod na expression na nag-uugnay ng kinetic energy at absolute temperature para sa ideal na gas:
mvcp2 / 2=3 / 2kB T.
Narito ang kB ay ang Boltzmann constant. Mula sa pagkakapantay-pantay na ito nakukuha natin ang:
T=m vcp2 / (3kB).
Universal equation of state
Kung pagsasamahin natin ang mga expression sa itaas para sa absolute pressure P at absolute temperature T, maaari nating isulat ang sumusunod na pagkakapantay-pantay:
PV=nRT.
Narito n ang dami ng substance sa mga moles, R ang gas constant na ipinakilala ni D. I. Mendeleev. Ang expression na ito ang pinakamahalagang equation sa teorya ng mga ideal na gas, dahil pinagsasama nito ang tatlong thermodynamic na parameter (V, P, T) at hindi nakadepende sa mga kemikal na katangian ng gas system.

Ang unibersal na equation ay unang-eksperimentong hinango ng French physicist na si Emile Clapeyron noong ika-19 na siglo at pagkatapos ay dinala sa modernong anyo ng Russian chemist na si Mendeleev, kung kaya't ito ay kasalukuyang nagtataglay ng mga pangalan ng mga siyentipikong ito.






