Natural na geometric na pattern o pattern ay lumalabas bilang umuulit na mga hugis na kung minsan ay maaaring ilarawan o kinakatawan ng mga mathematical na modelo.
Geometry sa kalikasan at buhay ay may maraming hugis at anyo, gaya ng simetrya, mga spiral o alon.
Kasaysayan
Sa unang pagkakataon, sinagot ng mga sinaunang pilosopo at siyentipikong Greek - Pythagoras, Empedocles at Plato - ang mga tanong tungkol sa geometry sa kalikasan. Sa pamamagitan ng pagsusuri ng mga halimbawa ng predictable o ideal na geometric na hugis sa mga halaman at hayop, sinubukan nilang ipakita ang kaayusan at simetriya sa kalikasan.
Ang mga modernong pagtatangka na pag-aralan ang geometry sa kalikasan ay nagsimula noong ika-19 na siglo sa pagsisikap ng Belgian physicist na si Joseph Plateau, na bumuo ng konsepto ng pinakamababang ibabaw ng isang bubble ng sabon. Ang mga unang modernong pagtatangka ay unang nakatuon sa pagpapakita ng perpekto at predictable na mga geometric na hugis, at pagkatapos ay bumaling sa pagbuo ng mga modelo na hinuhulaan ang hitsura at pagpapakita ng geometry sa kalikasan.
Noong ika-20 siglo, ang mathematician na si Alan Turing ay nagtrabaho sa mga mekanismo ng morphogenesis, na nagpapaliwanag sa hitsura ng mga hayopiba't ibang mga pattern, guhitan, mga spot. Makalipas ang ilang sandali, ang biologist na si Aristide Lindenmeier, kasama ang mathematician na si Benoit Mandelbrot, ay kumpleto sa gawain sa mga mathematical fractals na paulit-ulit ang mga pattern ng paglago ng ilang halaman, kabilang ang mga puno.
Science
Mga modernong agham (matematika, pisika at kimika), sa tulong ng mga teknolohiya at modelo, subukan hindi lamang ipaliwanag, kundi hulaan din ang mga geometric na pattern na matatagpuan sa kalikasan.
Ang hugis at kulay ng maraming buhay na organismo, tulad ng peacock, hummingbird at sea shells, ay hindi lamang maganda, kundi pati na rin ang geometrically correct, na umaakit sa curiosity ng mga siyentipiko. Ang kagandahang nakikita natin sa kalikasan ay maaaring natural, sa matematika.
Ang naobserbahang natural na mga pattern sa matematika ay ipinaliwanag ng chaos theory, na gumagana sa mga spiral at fractals. Ang ganitong mga pattern ay sumusunod sa mga batas ng physics, bilang karagdagan, ang physics at chemistry, gamit ang abstract mathematics, hinuhulaan ang mga hugis ng mga kristal, parehong natural at artipisyal.
Ipinapaliwanag ng biology ang geometry sa kalikasan sa pamamagitan ng natural selection, kung saan ang mga karaniwang katangian gaya ng mga guhit, batik, maliliwanag na kulay ay maaaring ipaliwanag sa pamamagitan ng pangangailangan para sa pagtatakip o pagpapadala ng mga signal.
Mga uri ng pattern
Sa kalikasan, maraming umuulit na pattern na lumilitaw sa iba't ibang geometric na hugis. Ang mga uri ng pangunahing regularidad ng geometry sa kalikasan, mga larawan at mga paglalarawan ng mga ito ay makikita sa ibaba.
Simetrya. Ang geometric na hugis na ito ay isa sa pinakakaraniwan sa kalikasan. Ang pinakakaraniwan sa mga hayopmirror symmetry - butterflies, beetles, tigre, owls. Ito ay matatagpuan din sa mga halaman, tulad ng mga dahon ng maple o mga bulaklak ng orchid. Bilang karagdagan, ang simetriko geometry sa kalikasan ay maaaring radial, five-ray o anim na beses, tulad ng mga snowflake.

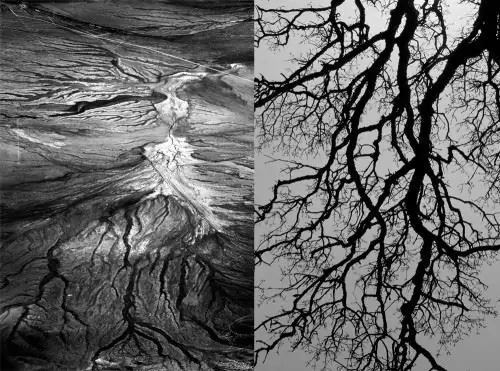
Fractals. Sa matematika, ang mga ito ay magkatulad na mga konstruksyon na walang katapusan. Sa likas na katangian, imposibleng makita ang gayong walang katapusang paulit-ulit na anyo, samakatuwid, ang mga pagtatantya ng mga pattern ng fractal ay tinatawag na geometric fractals sa kalikasan. Ang ganitong geometry ay makikita sa kalikasan sa mga dahon ng pako, broccoli, prutas ng pinya.
Spirals. Ang mga anyo na ito ay karaniwan lalo na sa mga mollusk at snail. Ang mga siyentipiko ay nagmamasid sa mga spiral na hugis sa kalawakan, halimbawa, spiral galaxies. Ang spiral ay tinatawag na golden ratio ng Fibonacci.

Meanders. Ang randomness ng mga dynamical system sa matematika ay nagpapakita ng sarili sa kalikasan sa mga anyo tulad ng meanders at flows. Ang natural na geometry ay nasa anyo ng isang putol o mas hubog na linya, gaya ng daloy ng ilog.
Mga alon. Ang mga ito ay sanhi ng mga kaguluhan at paggalaw ng hangin, mga alon ng hangin, na kumakalat kapwa sa pamamagitan ng hangin at sa pamamagitan ng tubig. Sa kalikasan, ang mga ito ay hindi lamang mga alon ng dagat, kundi pati na rin ang mga buhangin ng disyerto, na maaaring bumuo ng mga geometric na hugis - mga linya, gasuklay at parabola.
Mosaic. Nilikha sa pamamagitan ng pag-uulit ng parehong mga elemento sa ibabaw. Ang mosaic geometry sa wildlife ay matatagpuan sa mga bubuyog: nagtatayo silapugad ng pulot-pukyutan - umuulit na mga cell.

Pagbuo ng mga pattern
Sa biology, ang pagbuo ng isang geometric na kulay ay dahil sa proseso ng natural selection. Bumalik sa kalagitnaan ng ika-20 siglo, pinamamahalaang ni Alan Turing na ilarawan ang mekanismo para sa paglitaw ng mga spot at guhitan sa kulay ng mga hayop - tinawag niya itong modelo ng reaksyon-diffusion. Ang ilang mga selula ng katawan ay naglalaman ng mga gene na kinokontrol ng mga reaksiyong kemikal. Ang Morphogen ay humahantong sa pagbuo ng mga lugar ng balat na may madilim na pigment (mga spot at guhitan). Kung ang morphogen ay naroroon sa lahat ng mga selula ng balat - ang kulay ng panther ay nakuha, kung ito ay naroroon nang hindi pantay - ang karaniwang batik-batik na leopardo.






