Ang
Modulus of elasticity ay isang pisikal na dami na nagpapakilala sa elastic na pag-uugali ng isang materyal kapag ang isang panlabas na puwersa ay inilapat dito sa isang partikular na direksyon. Ang nababanat na pag-uugali ng isang materyal ay nangangahulugan ng pagpapapangit nito sa nababanat na rehiyon.
Kasaysayan ng pag-aaral ng pagkalastiko ng mga materyales

Ang pisikal na teorya ng mga nababanat na katawan at ang kanilang pag-uugali sa ilalim ng pagkilos ng mga panlabas na puwersa ay isinasaalang-alang nang detalyado at pinag-aralan ng Ingles na siyentipiko noong ika-19 na siglo, si Thomas Young. Gayunpaman, ang mismong konsepto ng pagkalastiko ay binuo noong 1727 ng Swiss mathematician, physicist at pilosopo na si Leonhard Euler, at ang mga unang eksperimento na may kaugnayan sa modulus of elasticity ay isinagawa noong 1782, iyon ay, 25 taon bago ang gawain ni Thomas Jung, ng Venetian mathematician at pilosopo na si Jacopo Ricatti.
Ang merito ni Thomas Young ay nakasalalay sa katotohanan na binigyan niya ang teorya ng elasticity ng isang payat na modernong hitsura, na pagkatapos ay ginawang pormal sa anyo ng isang simple at pagkatapos ay pangkalahatan na batas ni Hooke.
Pisikal na katangian ng pagkalastiko
Anumang katawan ay binubuo ng mga atomo, kung saan kumikilos ang mga puwersa ng pang-akit at pagtanggi. Ang balanse ng mga puwersang ito ayang estado at mga parameter ng bagay sa ilalim ng mga ibinigay na kondisyon. Ang mga atomo ng isang solidong katawan, kapag ang mga hindi gaanong panlabas na puwersa ng pag-igting o compression ay inilapat sa kanila, ay nagsisimulang maglipat, na lumilikha ng puwersa na kabaligtaran sa direksyon at pantay sa magnitude, na may posibilidad na ibalik ang mga atomo sa kanilang orihinal na estado.
Sa proseso ng naturang paglilipat ng mga atomo, tumataas ang enerhiya ng buong sistema. Ipinapakita ng mga eksperimento na sa maliliit na strain ang enerhiya ay proporsyonal sa parisukat ng mga strain na ito. Nangangahulugan ito na ang puwersa, bilang isang derivative na may paggalang sa enerhiya, ay lumalabas na proporsyonal sa unang kapangyarihan ng strain, iyon ay, ito ay nakasalalay sa linearly dito. Pagsagot sa tanong, ano ang modulus ng pagkalastiko, masasabi nating ito ang koepisyent ng proporsyonalidad sa pagitan ng puwersa na kumikilos sa atom at ang pagpapapangit na sanhi ng puwersang ito. Ang dimensyon ng modulus ni Young ay kapareho ng dimensyon ng presyon (Pascal).
Elastic na limitasyon
Ayon sa kahulugan, ang modulus of elasticity ay nagpapahiwatig kung gaano karaming stress ang dapat ilapat sa isang solid upang maging 100% ang deformation nito. Gayunpaman, ang lahat ng solid ay may nababanat na limitasyon na katumbas ng 1% strain. Nangangahulugan ito na kung ang isang naaangkop na puwersa ay inilapat at ang katawan ay deformed ng isang halaga na mas mababa sa 1%, pagkatapos pagkatapos ng pagwawakas ng puwersa na ito, ang katawan ay eksaktong ibinalik ang orihinal na hugis at sukat nito. Kung masyadong maraming puwersa ang inilapat, kung saan ang halaga ng pagpapapangit ay lumampas sa 1%, pagkatapos ng pagwawakas ng panlabas na puwersa, hindi na ibabalik ng katawan ang mga orihinal na sukat nito. Sa huling kaso, ang isa ay nagsasalita ng pagkakaroon ng isang natitirang pagpapapangit, na kung saan ayebidensya na nalampasan na ang elastic na limitasyon ng materyal.
Young's modulus in action
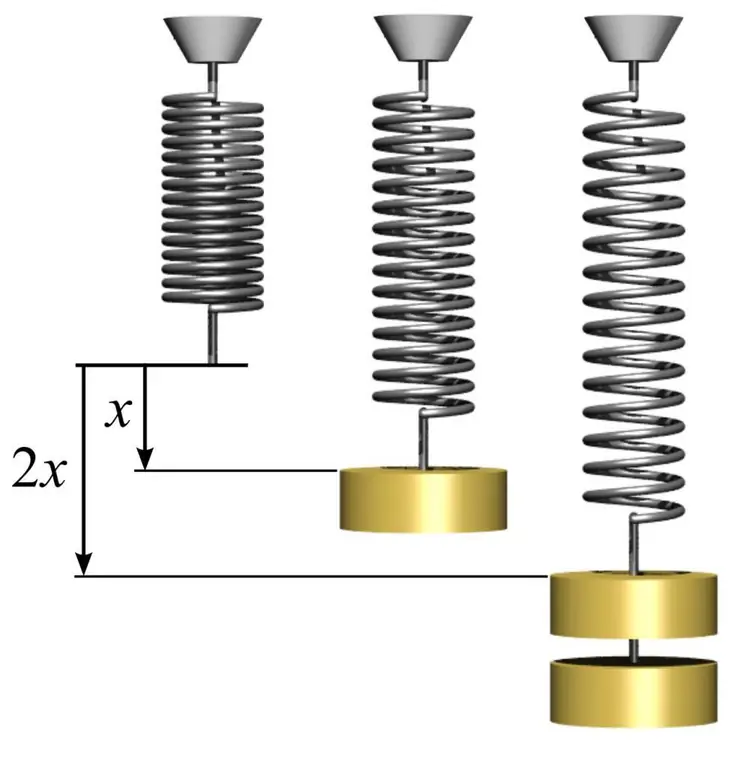
Upang matukoy ang modulus ng elasticity, pati na rin upang maunawaan kung paano ito gamitin, maaari kang magbigay ng isang simpleng halimbawa sa isang spring. Upang gawin ito, kailangan mong kumuha ng metal spring at sukatin ang lugar ng bilog na nabuo ang mga coils nito. Ginagawa ito gamit ang simpleng formula na S=πr², kung saan ang n ay pi katumbas ng 3.14 at ang r ay ang radius ng coil ng spring.
Susunod, sukatin ang haba ng spring l0 nang walang load. Kung magsabit ka ng anumang load ng mass m1 sa isang spring, tataas ang haba nito sa isang partikular na halaga l1. Ang modulus ng elasticity E ay maaaring kalkulahin batay sa kaalaman sa batas ni Hooke sa pamamagitan ng formula: E=m1gl0/(S(l 1-l0)), kung saan ang g ay ang free fall acceleration. Sa kasong ito, tandaan namin na ang dami ng deformation ng spring sa nababanat na rehiyon ay maaaring higit na lumampas sa 1%.
Ang pag-alam sa modulus ng Young ay nagbibigay-daan sa iyong mahulaan ang dami ng deformation sa ilalim ng pagkilos ng isang partikular na stress. Sa kasong ito, kung isabit natin ang isa pang mass m2 sa spring, makukuha natin ang sumusunod na value ng relative deformation: d=m2g/ (SE), kung saan ang d - relatibong deformation sa nababanat na rehiyon.
Isotropy at anisotropy
Ang modulus of elasticity ay isang katangian ng isang materyal na naglalarawan sa lakas ng bono sa pagitan ng mga atom at molekula nito, gayunpaman ang isang partikular na materyal ay maaaring magkaroon ng ilang iba't ibang moduli ng Young.
Ang katotohanan ay ang mga katangian ng bawat solid ay nakasalalay sa panloob na istraktura nito. Kung ang mga katangian ay pareho sa lahat ng spatial na direksyon, kung gayon pinag-uusapan natin ang tungkol sa isang isotropic na materyal. Ang mga naturang sangkap ay may isang homogenous na istraktura, kaya ang pagkilos ng isang panlabas na puwersa sa iba't ibang direksyon sa kanila ay nagiging sanhi ng parehong reaksyon mula sa materyal. Ang lahat ng amorphous na materyales ay isotropic, gaya ng goma o salamin.
Ang
Anisotropy ay isang phenomenon na nailalarawan sa pamamagitan ng pagdepende ng mga pisikal na katangian ng isang solid o likido sa direksyon. Ang lahat ng mga metal at haluang metal batay sa mga ito ay may isa o isa pang kristal na sala-sala, iyon ay, isang nakaayos, sa halip na isang magulong pag-aayos ng mga ionic core. Para sa mga naturang materyales, ang modulus ng elasticity ay nag-iiba depende sa axis ng pagkilos ng panlabas na stress. Halimbawa, ang mga metal na may cubic symmetry, gaya ng aluminum, copper, silver, refractory metals, at iba pa, ay may tatlong magkakaibang Young's moduli.
Shear modulus
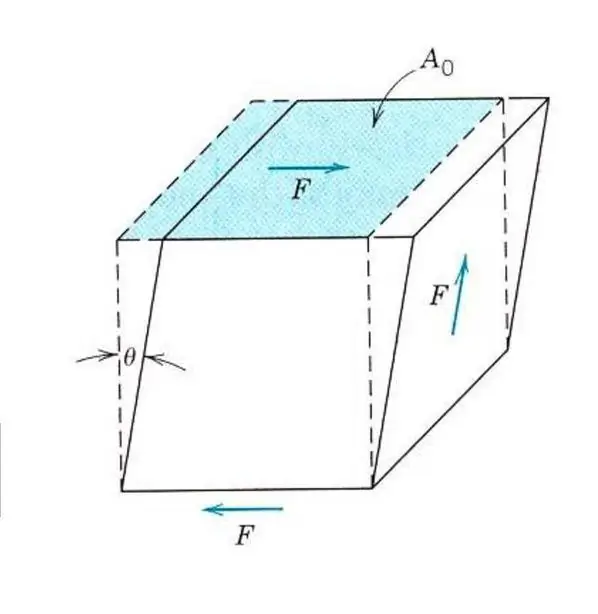
Paglalarawan ng mga elastic na katangian ng kahit isang isotropic na materyal ay hindi nangangailangan ng kaalaman sa isang Young's modulus. Dahil, bilang karagdagan sa pag-igting at compression, ang materyal ay maaaring maapektuhan ng mga paggugupit na stress o torsional stress. Sa kasong ito, iba ang magiging reaksyon nito sa panlabas na puwersa. Upang ilarawan ang elastic shear deformation, isang analogue ng Young's modulus, shear modulus, o modulus of elasticity ng pangalawang uri ay ipinakilala.
Lahat ng materyales ay lumalaban sa shear stress na mas mababa sa tension o compression, kaya ang shear modulus value para sa mga ito ay 2-3 beses na mas mababa kaysa sa value ng Young's modulus. Kaya, para sa titanium, na ang modulus ng Young ay katumbas ng 107 GPa, ang shear modulus ay40 GPa lang, para sa bakal ang mga figure na ito ay 210 GPa at 80 GPa, ayon sa pagkakabanggit.
Modulus of elasticity of wood

Ang kahoy ay isang anisotropic na materyal dahil ang mga hibla ng kahoy ay nakatuon sa isang tiyak na direksyon. Nasa kahabaan ng mga hibla na sinusukat ang modulus ng elasticity ng kahoy, dahil ito ay 1-2 order ng magnitude na mas maliit sa mga hibla. Ang kaalaman sa modulus ni Young para sa kahoy ay mahalaga at isinasaalang-alang kapag nagdidisenyo ng mga istruktura ng wood panel.
Ang mga halaga ng modulus of elasticity ng kahoy para sa ilang uri ng puno ay ipinapakita sa talahanayan sa ibaba.
| Tree view | Modulus ni Young sa GPa |
| Laurel tree | 14 |
| Eucalyptus | 18 |
| Cedar | 8 |
| Spruce | 11 |
| Pine | 10 |
| Oak | 12 |
Dapat tandaan na ang mga value na ibinigay ay maaaring mag-iba ng hanggang 1 GPa para sa isang partikular na puno, dahil ang Young's modulus nito ay apektado ng density ng kahoy at mga kondisyon ng paglaki.

Shear moduli para sa iba't ibang species ng puno ay nasa hanay na 1-2 GPa, halimbawa, para sa pine ito ay 1.21 GPa, at para sa oak 1.38 GPa, iyon ay, ang kahoy ay halos hindi lumalaban sa shear stresses. Ang katotohanang ito ay dapat isaalang-alang sa paggawa ng mga kahoy na istrukturang nagdadala ng pagkarga, na idinisenyo upang gumana lamang sa pag-igting o compression.
Elastic na katangian ng mga metal
Kung ihahambing sa Young's modulus ng kahoy, ang mga average na halaga ng halagang ito para sa mga metal at haluang metal ay isang pagkakasunod-sunod ng magnitude na mas malaki, tulad ng ipinapakita sa sumusunod na talahanayan.
| Metal | Modulus ni Young sa GPa |
| Bronze | 120 |
| Copper | 110 |
| Bakal | 210 |
| Titanium | 107 |
| Nikel | 204 |
Ang nababanat na katangian ng mga metal na may kubiko na syngony ay inilalarawan ng tatlong elastic constant. Ang mga naturang metal ay kinabibilangan ng tanso, nikel, aluminyo, bakal. Kung ang isang metal ay may hexagonal syngony, kailangan na ng anim na constant para ilarawan ang mga katangiang elastiko nito.
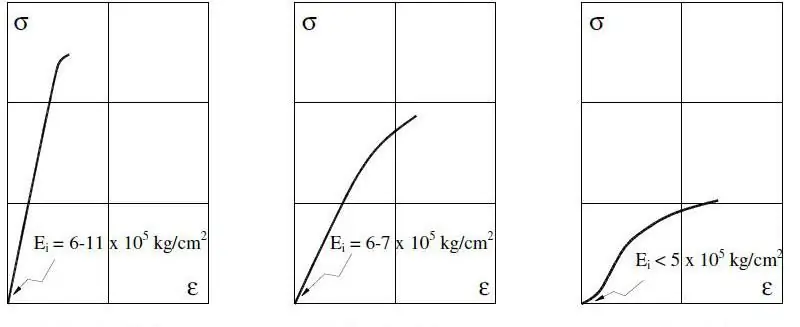
Para sa mga metallic system, ang modulus ni Young ay sinusukat sa loob ng 0.2% strain, dahil ang malalaking value ay maaaring mangyari sa inelastic na rehiyon.






