Habang tumatanda ang mga mag-aaral, mas kailangan ang bilis sa paglutas ng mga simpleng problema. Hindi gaanong oras ang ibinibigay sa mga pagsusulit upang malutas ang mga simpleng halimbawa o problema sa mahabang panahon. Paano mahanap ang dayagonal ng isang parisukat nang mabilis at madali? Ito ay itinuro sa mga bata mula sa ikawalong baitang. Ang artikulong ito ay nagpapakita ng dalawang paraan - ang isa ay mas mahaba, ang isa ay mas mabilis.
Paano kalkulahin ang dayagonal ng isang parisukat?
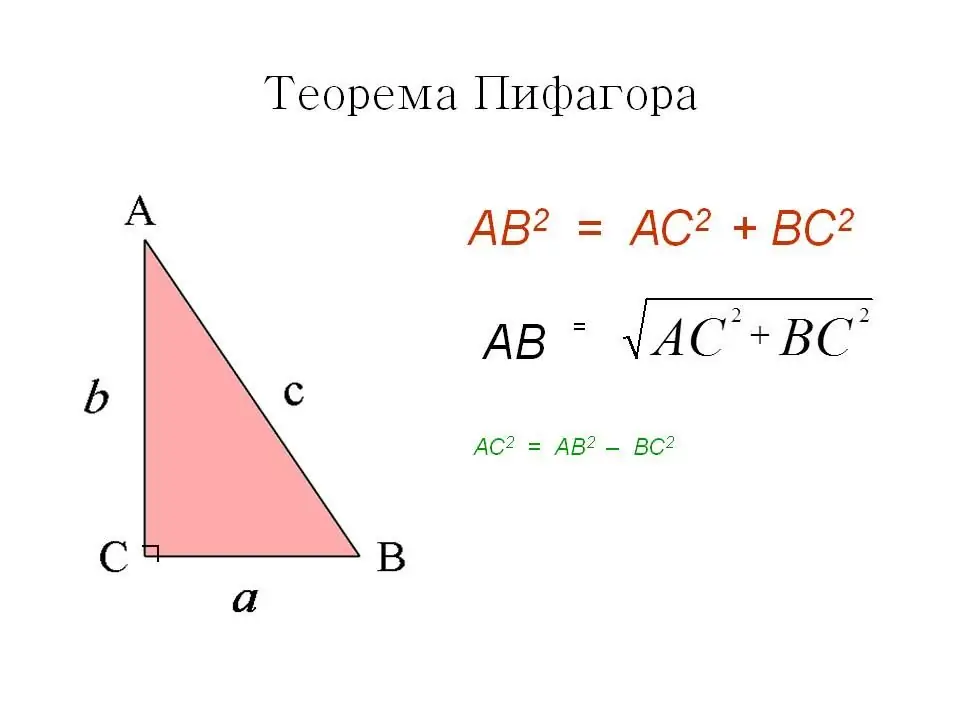
Ang unang paraan ay ang kilala at pamilyar na Pythagorean theorem. Sa isang parisukat, ang lahat ng mga anggulo ay tama, na nangangahulugan na ang dayagonal ay nahahati ito sa dalawang magkaparehong right-angled na tatsulok at ito mismo ang kanilang hypotenuse. Ayon sa Pythagorean theorem, ang parisukat ng hypotenuse ay katumbas ng kabuuan ng mga parisukat ng mga binti.

Ang pangalawang paraan ay isang simpleng formula na natatangi sa mga parisukat, at kailangan mo lang itong tandaan. Tulad ng alam mo, ang lahat ng panig ng isang parisukat ay pantay-pantay, at iyon ang dahilan kung bakit kinakalkula ng mga mathematician ang sumusunod na formula para sa paghahanap ng dayagonal nito: ito ay katumbas ng produkto ng gilid at ang ugat ng dalawa.
Siyempre, pinakamahusay na tandaan ang formula para sa haba ng dayagonal ng isang parisukat at gamitin ito palagi, dahil ito ay mas mabilis at mas maginhawa. Lalo itong nararamdaman kapag nilulutas ang mga problema sa literal na anyo, kung saan sa halip na buong malalaking root expression, maaari kang makayanan gamit ang isang produkto lamang.
Halimbawa
Kunin, halimbawa, ang isang 6 by 6 square, ibig sabihin, may gilid na katumbas ng anim na sentimetro.
Ayon sa unang paraan: hayaang C ang dayagonal, at A ang gilid.
Pagkatapos ay makukuha natin na C=√A^2+A^2 o C=√2A^2.
Isulat natin ito sa numerical form: С=√36 + 36. Nakakuha tayo ng √72, which is 3√8 o 6√2.
At ngayon hanapin natin ang parehong dayagonal, ngunit sa pangalawang paraan: C=A√2 o sa numerical form: 6√2
Ngayon ay makikita mo na kung gaano ang pangalawang paraan ay mas mabilis, mas madali at pinakamahalaga - mas mahusay, lalo na sa mga ganitong madaling problema, dahil ang bawat minuto ay mahalaga sa pagsusulit!
Iba pang katangian ng mga square diagonal
Bukod sa pag-alam kung paano hanapin ang mga diagonal ng isang parisukat, kailangan mo ring malaman ang kanilang mga katangian. Ang mga pangunahing ay:
- Ang mga diagonal ay pantay sa isa't isa at ang intersection point ay nahahati sa kalahati.
- Bumubuo sila ng mga tamang anggulo kapag nagsalubong sila.
- Hatiin ang parisukat sa pantay na tatsulok.
Konklusyon
Ang tanong kung paano mabibilang ang mga dayagonal ng isang parisukat ay karaniwang itinatanong ng mga mag-aaral na hindi nakuha ang paksang ito sa paaralan. Gayunpaman, dapat malaman ng lahat ang mga pangunahing tuntunin ng matematika! Ito ay kanais-nais na malutas sa lalong madaling panahon, at ito ay nangangailangan ng kaalaman sa mga pinaikling formula. Ang lahat ng ito ay sobrang simple at madali, ngunitsa parehong oras, ito ang batayan na kinakailangan para sa paglutas ng mas kumplikadong mga problema sa hinaharap. At isang mahalagang bahagi ng base na ito ay ang parisukat.






